Les tables de décision sont utilisées lorsque le système décisionnel se présente sous la forme d'un triplet : (conditions, règles, actions). Dans d'autres cas, un système décisionnel se présente comme une suite d'étapes exigeant chacune une décision. L'objectif est alors de trouver le chemin répondant à certaines contraintes.
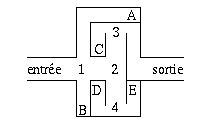
L'exemple le plus classique est le parcours d'un labyrinthe. A chaque carrefour, il faut choisir une nouvelle direction. Si la direction choisie ne mène pas à la solution, il faut pouvoir revenir au carrefour précédent et essayer une autre direction.

Fig. 15.8. Les chiffres indiquent les points où une décision doit être prise. Les lettres désignent les culs-de-sac.
Si l'on exclut la possibilité de revenir sur ses pas, on peut représenter le cheminement à l'intérieur du labyrinthe par l'arbre de la figure 15.9.
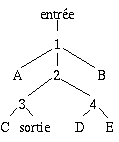
Fig. 15.9. Arbre de décision pour le parcours d'un labyrinthe, sans retour en arrière.
Si on lève la restriction d'un retour possible en arrière, l'arbre prend alors la forme suivante :
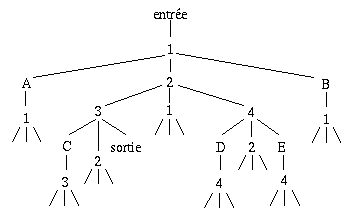
Fig. 15.10. Arbre de décision avec retour en arrière.
Le même noeud peut apparaître plusieurs fois à plusieurs endroits dans l'arbre indiquant ainsi qu'il existe plusieurs chemins pour l'atteindre. Dans de tels cas, il est intéressant de pouvoir déterminer quel est le plus court chemin d'un point à l'autre. De plus, l'arbre est devenu infini étant donné la possibilité de visiter un point un nombre indéterminé de fois.
Pour une représentation efficace, on abandonne alors la structure d'arbre au profit de celle de graphe. Une telle situation se présente souvent dans des jeux de pièces (échecs par exemple) où les mouvements des pièces permettent de créer la même configuration à plusieurs reprises. C'est pourquoi les règles interdisent souvent de reproduire plus de n fois la même configuration.
Ayant pris l'exemple de jeux, on est amené tout naturellement à se demander comment représenter l'évolution d'un jeu comme : les échecs, les dames, tic-tac-toe, nim, etc, mettant aux prises deux adversaires.
Prenons comme exemple le jeu de nim. Soit un tas de n allumettes, les
règles sont les suivantes :
La figure 15.11 représente les situations possibles du jeu de nim pour n = 6 allumettes.
Une configuration du jeu est entièrement déterminée par le nombre d'allumettes dans le tas. A tout instant l'état du jeu est donné par la configuration et l'indication du joueur dont c'est le tour. Une configuration finale d'un jeu représente le gain, la perte du jeu ou un match nul. Tout autre configuration est non-terminale. Dans le jeu de nim il n'y a qu'une configuration finale possible : lorsqu'il ne reste plus d'allumette sur le tas.
Les arbres de jeu sont utiles pour déterminer quel est le meilleur mouvement qu'un joueur doit faire. Dans la figure 15.11, le joueur A est au départ dans la situation où 3 possibilités s'offrent à lui; laquelle doit-il prendre s'il veut gagner ?
Il doit choisir celle qui maximise ses chances de victoire.
Pour pouvoir faire ce choix, il faut pouvoir évaluer, parmi les différentes situations possibles, celle qui est la meilleure. On peut pour cela utiliser une fonction d'évaluation E(x) qui associe une valeur numérique à toute configuration x du jeu. Cette fonction est une mesure de la valeur d'une configuration pour un joueur donné.
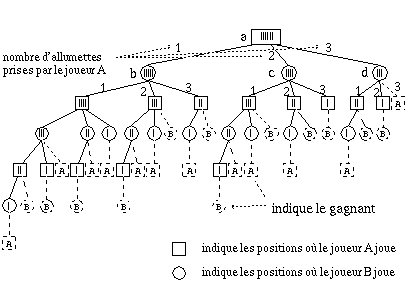
Fig. 15.11. Situations possibles pour le jeu de nim.
Cette fonction E(x) doit donner une valeur élevée lorsque le joueur a une bonne chance de gagner et une valeur basse lorsqu'il a une faible chance de gagner (ou lorsque son adversaire a une grande chance de gagner).
Ainsi, pour l'arbre de la figure 15.11, il est facile d'imaginer une fonction E(x) pour une configuration finale (du point de vue du joueur A) :
| E(x)= | { | 1 si x est une configuration pour A |
| -1 si x est une configuration perdante pour A |
Partant de cette indication, quel mouvement (b, c ou d sur la figure) A doit-il faire au départ? Pour cela il faut évaluer les configurations b, c, d respectivement et déterminer quelle est la meilleure. Il s'avère que le mouvement gagnant est b, car c'est une position à partir de laquelle A peut gagner indépendamment des mouvements de B.
Comment évaluer la valeur d'une position intermédiaire x? Cette évaluation repose sur les valeurs des positions suivantes; ainsi comme les tours de jeu se font en alternance pour A et B, une position gagnante pour A est une position perdante pour B. La fonction d'évaluation exprimant la valeur d'une configuration pour un joueur donné, et toujours pour ce même joueur, on peut l'exprimer dans le cas de notre exemple par la formule suivante, appelée formule du minimax:
| V(x)= | { | max (V(ci)) si x est un carré 1<i<d |
| min(V(ci)) si x est un rond 1<i<d |
avec d = degré du noeud x (c.à.d. le nombre de ses descendants).
Dans le cas de ce jeu, le nombre de configurations possibles, à partir d'une configuration de départ (la configuration vide), est très grand : pour 3 x 3 cases, on a 9! configurations possibles (362'880). Ce nombre peut être réduit si l'on tient compte des symétries du jeu, comme le montre la figure 15.12.
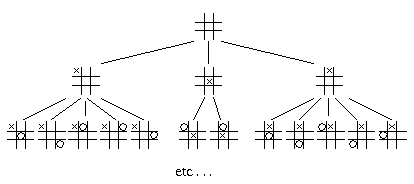
Fig. 15.12. Début de l'arborescence de décision.
Quelle fonction d'évaluation peut-on considérer pour ce jeu ?
Si le joueur X est pris comme joueur de référence (c'est celui qui commence le jeu), on peut déterminer une valeur V comme :
V = V1 - V2
où V1 est la somme de :
Exemple
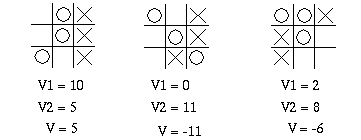
Fig. 15.13. Différentes configurations de jeu avec fonction d'évaluation correspondante.
Autre possibilité :
V1= nombre de lignes, colonnes et diagonales encore ouvertes pour
X
V2= nombre de lignes, colonnes et diagonales encore ouvertes pour
O
 15.3. Réalisation
d'une procédure MiniMax
15.3. Réalisation
d'une procédure MiniMax
Site Hosting: Bronco