Dans les deux méthodes de recherche examinées jusqu'ici, la recherche s'effectuait en parcourant le tableau selon une méthode systématique (en éliminant à chaque fois la moitié des éléments possibles, ou en parcourant tous les éléments dans l'ordre).
Dans le but de construire un algorithme encore plus efficace, il serait très intéressant de pouvoir déterminer l'adresse où se trouve (ou devrait se trouver) la clé K recherchée, en fonction de K elle-même. Une telle méthode éviterait d'examiner des positions inintéressantes du tableau et localiserait immédiatement la clé recherchée.
Cependant, on a généralement un nombre N de valeurs de clés possibles beaucoup plus grand que le nombre de composantes du tableau. Dans un tel cas il ne peut y avoir de correspondance une à une entre valeur d'une clé et composante du tableau, c'est-à-dire avoir une position différente du tableau pour chaque valeur possible de la clé. Par conséquent, quelques sous- ensembles de deux ou de plusieurs clés possibles correspondront forcément à la même position du tableau.
Ainsi, si on a deux clés K1 et K2 et une adresse A dans le tableau telle que :
H(K1) = A = H(K2)
On dira que K1 et K2 sont en collision sur l'adresse A par la fonction de transformation H.
Pour réaliser un bon algorithme de stockage et de recherche d'information par une méthode de "hash-coding", il faut déterminer deux choses :
Il n'existe pas de fonction de hash-code universelle qui soit bonne dans n'importe quel contexte. Si l'on ne sait rien de la distribution des clés K, on choisira une fonction H qui donne une distribution uniforme des valeurs H(k), avec l'hypothèse que toutes les clés K soient équiprobables.
D'un autre côté, si l'on connaît la distribution des clés K, on pourra alors déterminer une fonction H dépendante de cette distribution et qui assigne des positions séparées à des groupes de clés
De plus, si l'on connaît à l'avance toute les clés qui doivent être stockées dans le tableau, il existe des techniques pour déterminer une fonction de hash-code parfaite, qui ne provoquera donc aucune collision. Ces techniques sont relativement complexes et coûteuses en temps de calcul, mais les fonctions ainsi produites sont généralement simples et rapides.
Ces fonctions de hash-code parfaites sont parfois employées dans les compilateurs pour retrouver très rapidement si un identificateur est un mot réservé du langage ou si c'est un identificateur défini par l'utilisateur. Les mots réservés d'un langage sont en effet fixés une fois pour toutes et sont donc connus à l'avance.
Même si l'on a des fonctions H parfaitement uniformes, la probabilité d'une collision est grande, sauf pour des tableaux très faiblement occupés. Par exemple, on peut faire un parallèle avec le paradoxe de l'anniversaire, qui dit que parmi 23 personnes ou plus, la probabilité que 2 personnes aient leur anniversaire le même jour est supérieure à 50 %, et que si l'on a plus de 88 personnes la probabilité est la même que 3 personnes aient leur anniversaire le même jour.
Transposé à notre problème, cela signifie que, pour un tableau de 365 positions, contenant 88 clés ou plus, dont les adresses ont été calculées uniformément et aléatoirement, on aura plus de 50 % de chance d'avoir une collision de deux ou trois clés à la même adresse.
Parmi les nombreuses méthodes de traitement des collisions, nous en retiendrons deux :
Cette méthode est la plus simple. Elle consiste à déclarer un tableau de pointeurs, de façon à pouvoir construire, à partir de chaque position du tableau, une chaîne qui contient toutes les clés qui ont été envoyées par la fonction H sur cette adresse. Il est possible d'organiser la chaîne par ordre croissant ou décroissant des clés, ce qui permet d'optimiser la recherche ultérieure d'une clé donnée.
La procédure suivante permet d'initialiser un tel tableau :
const MaxElements = ...;
MaxIndice = MaxElements-1;
type Lien = ^Noeud;
Noeud = record
Cle : integer;
Info : integer;
Suivant : Lien;
end; { Noeud }
var Tableau: array [0..MaxIndice] of Lien;
procedure Initialisation;
var i : integer;
begin
for i := 0 to MaxIndice do
Tableau[i] := nil;
end; { Initialisation }
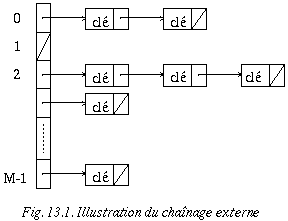
La figure 13.1 illustre la structure utilisée pour le chaînage externe. On peut noter que certaines entrées du tableau correspondent à une chaîne vide.
Les procédures d'insertion et de recherche vues dans le chapitre sur les chaînes s'appliquent sans autre dans le cas du traitement des collisions par chaînage externe. Dans l'exemple qui suit, nous supposerons que les clés sont de simples caractères et que chaque occurrence d'une même clé doit être stockée séparément (pour simuler les collisions). La chaîne associée à chaque entrée du tableau est indiquée verticalement en dessous de l'entrée correspondante.
k : C E C I E S T U N E X E M P L E
ord(k) : 3 5 3 9 5 19 20 21 14 5 24 5 13 16 12 5
H(k) : 3 5 3 9 5 8 9 10 3 5 2 5 2 5 1 5
H(k) = ord(k) mod M et M = 11 (dimension du tableau)
La structure de donnée correspondante peut être illustrée de la manière suivante :
D'autres alternatives existent quant à l'organisation d'un tableau de h-coding avec chaînage externe. Par exemple :
Ce qui donnerait pour notre exemple la structure de la figure 13.4.
Si le nombre d'éléments à placer dans le tableau est
déterminé par avance, il est alors possible d'éviter
de mettre une partie des éléments à l'extérieur
du tableau (par chaînage). Plusieurs méthodes ont été
proposées pour stocker par hash-coding N éléments dans
un tableau de dimension M 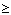 N, en utilisant les
positions inoccupées pour recevoir les éléments qui
collisionnent. Ce sont les méthodes dites de l'adressage ouvert.
N, en utilisant les
positions inoccupées pour recevoir les éléments qui
collisionnent. Ce sont les méthodes dites de l'adressage ouvert.
Les méthodes d'adressage ouvert pour résoudre des collisions peuvent se représenter à l'aide de l'algorithme général suivant :
var T : array[0 .. M] of Element;
Etat : (Trouve, PasTrouve, Recherche);
h0 := H(k);
i := 0;
hi := h0;
Etat := Recherche;
repeat
if T[hi].Cle = k then Etat := Trouve
else if T[hi].Cle = Vide then
Etat := PasTrouve
else begin {traitement d'une collision}
i := i+1;
hi := (h0 + G(i)) mod (M+1)
end { else }
until (Etat <> Recherche) or (i = M);
case Etat of
Trouve : { modif. de T[hi] possible };
PasTrouve: { insertion en T[hi] };
Recherche: { insertion impossible, table pleine };
end; { case }
Plusieurs façons de réaliser l'adressage ouvert sont possibles.
On inspecte les positions suivantes en partant de h0 et en supposant le tableau circulaire avec :
G(i) = i
ce qui donne :
h0 = H(k)
hi = (h0 + i) mod (M+1) ( mod : pour rendre le tableau circulaire)
Cette solution présente l'inconvénient de favoriser la création d'amas autour des indices primaires (cf. exemple de la figure 13.5).
Dans le cas idéal il faudrait que la fonction G(i) répartisse les indices secondaires hi aussi uniformément que possible sur les autres positions du tableau; mais cela est trop complexe et parfois trop coûteux. Un bon compromis est la solution quadratique qui vise à éloigner les points de collision le plus loin possible de l'indice primaire en fonction de l'ordre de la collision.
On choisit alors : G(i) = i2
Il faut noter que cette solution ne permet de parcourir que la moitié des positions du tableau. Il y a donc le risque de ne pas pouvoir placer un nouvel élément, même s'il existe une place libre dans le tableau. Il suffit, en effet, que cette place libre se trouve dans la moitié du tableau qui n'est pas parcourue.
Le fait que seule une moitié du tableau est parcourue tient à l'utilisation de la fonction Modulo pour simuler la circularité. On peut en effet démontrer que la i-ème collision fournit la même position que la (M-i)-ème collision (on suppose ici que l'intervalle d'indices est 0..M-1):
(h0 + i2) mod M = (h0 + (M-i)2) mod M
Il suffit pour cela de développer (M-i)2, qui donne M2-2iM+i2, soit (M-2i)M + i2. Or (x+yM) mod M = x du fait que le modulo consiste en le reste de la division entière. On obtient donc bien :
(h0 + (M-i)2) mod M = (h0 + ((M-2i)M+i2) mod M = (h0 + i2) mod M
Exemple : Algorithme d'insertion dans une table de h-code avec traitement linéaire des collisions.
const MaxElements = ...;
MaxIndice = MaxElements-1;
CleCaseVide = MaxInt;
type Element = record
Cle : integer;
Info : .....;
end; { Element }
var T: array[0..MaxIndice] of Element;
function H(k : integer) : integer;
begin
H := k mod MaxElements;
end; { H }
procedure Initialisation;
var i: integer;
begin
for i := 0 to MaxIndice do
T[i].Cle := CleCaseVide;
end; { Initialisation }
function Insert(X:integer,I:Info) :integer;
var H0, hi : integer;
begin
H0 := H(X);
hi := H0;
while (T[hi].Cle <> CleCaseVide) and
(T[hi].Cle <> X) do begin
hi := (hi+1) mod MaxElements;
if hi = H0 then begin
writeln('tableau plein');
exit(program);
end; { if }
end; { while }
if T[Hi].Cle = CleCaseVide then begin
T[hi].Cle := X;
T[Hi].Information := I;
end; { if }
Insert := hi;
end; { Insert }
Exemple : Soit la suite suivante de clés alphabétiques k :
k : C E C I E S T U N E X E M P L E ord(k): 3 5 3 9 5 19 20 21 14 5 24 5 13 16 12 5 H(k) : 3 5 3 9 5 0 1 2 14 5 5 5 13 16 12 5
N = 16 (Nombre de clés)
M = 19 : dimension du tableau qui doit être > N
H(k) = k mod M.
L'insertion des clés dans le tableau s'effectue selon la figure 13.5 (les [] indiquent les positions examinées pour effectuer l'insertion). On voit, sur cet exemple la conséquence de la formation d'amas qui est d'obliger à consulter des positions de valeurs d'indices primaires différentes avant de trouver des positions libres. En l'occurrence, l'insertion du 4ème 'E' nécessite l'examen des positions occupées par X et I de h-code différents.
Il existe une troisième possibilité pour un traitement des collisions par adressage ouvert; c'est celle qui consiste à calculer une seconde fonction de H-code pour déterminer le déplacement. Cette méthode est appelée double-h-code.
La deuxième fonction de h-code, H2(k), doit être choisie avec certaines précautions. Par exemple :
Par rapport à une fonction H1(k) = k mod M telle que nous l'avons envisagée dans les exemples, on peut considérer que la fonction
H2(k) = 1+( k mod (M-2))
constitue une bonne deuxième fonction de h-code si M et M-2 sont tous deux premiers. Le traitement des collisions par double-h-code est, en quelque sorte, un traitement personnalisé de la collision d'une clé k en fonction de la valeur de cette clé !
Il existe d'autres méthodes de traitement de collisions faisant intervenir des algorithmes plus complexes, mais, dans la plupart des cas, les méthodes décrites ici suffisent à résoudre les collisions de manière satisfaisante.
Quelle que soit la variante d'adressage ouvert utilisée, on peut essayer de réduire le nombre d'éléments ayant subi une collision en donnant la priorité à un nouvel élément sur un élément déjà présent dans le tableau si ce dernier a déjà subi une collision et n'est donc pas placé conformément à la valeur de son h-code. Cela implique, pour la solution quadratique, de retrouver le nombre de collisions déjà subies par l'élément du tableau à déplacer, étant donné que les déplacements sont fonction du nombre de collisions.
Pour plus de détails sur les différentes méthodes de traitement de collisions, consulter :
D.E. Knuth
"The Art of Computer Programming",
vol. III, Sorting and Searching, pp. 506-549
 13.5 Les fonctions
de h-code
13.5 Les fonctions
de h-code
Site Hosting: Bronco