Pour bien des applications impliquant des graphes orientés, on doit tenir compte des graphes cycliques.
Si, par exemple, un graphe orienté représente un processus de production, que les noeuds sont les opérations à effectuer et que les arcs sont les indications de l'ordre dans lequel ces opérations sont à faire, alors la présence d'un cycle traduit une incohérence du modèle. En effet, dire que l'opération A précède l'opération G qui précède l'opération C qui précède l'opération A n'a aucun sens (cf. graphe précédent en 11.2.).
Il faut donc que l'on utilise, pour de telles applications, des graphes orientés acycliques.
Définition : un graphe orienté est acyclique si, pour n'importe quel sommet de départ, il est impossible de retomber sur ce sommet en suivant le sens des arcs.
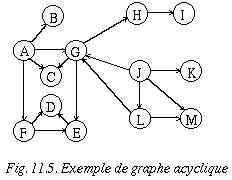
Ainsi, en faisant quelques simplifications (suppression de certains arcs et inversion du sens de certains autres) il est possible de transformer notre graphe-exemple en un graphe acyclique (figure 11.5).
Vu de n'importe quel sommet, en suivant le sens des arcs, un graphe orienté acyclique se présente comme un arbre. Cela ne signifie pas qu'un graphe orienté acyclique est un arbre, mais plutôt que les arcs et sommets accessibles depuis un sommet donné se présentent comme une structure d'arbres (figure 11.6).
Cela implique que les arbres de parcours par DFS d'un graphe orienté acyclique ne possèdent pas de pointeurs "vers le haut", ce qui est le critère utilisé pour vérifier qu'un graphe orienté est acyclique ou pas. Ainsi, pour notre graphe exemple, l'algorithme DFS produit (à partir du sommet A) l'arbre de parcours de la figure 11.7. Il n'y a pas de pointeurs vers un noeud ancêtre. Il n'y a donc pas de cycle.
Une opération importante pour les graphes orientés acycliques est de considérer ses sommets dans un ordre tel qu'aucun sommet n'est traversé avant que les sommets qui pointent vers lui n'aient été déjà traversés. Pour notre graphe-exemple, la suite de sommets
J K L M A G H I F E D B C
satisfait une telle condition. Si on voulait représenter les arcs sur une telle liste, ils iraient tous de gauche à droite (figure 11.8.).
Comme indiqué précédemment une telle représentation a des applications évidentes dans les domaines de séquencement d'opération.
L'opération qui consiste à établir une telle représentation est appelée le tri topologique.
Il faut relever qu'il y a souvent plusieurs solutions pour le tri topologique d'un graphe orienté acyclique. Par exemple A J L G F K E M B H C I D est aussi un ordre topologique pour notre graphe-exemple.
Nous ne donnerons pas d'exemple d'algorithme de tri topologique car il est généralement plus facile de faire un tri topologique inverse.
 11.5. Tri topologique
inverse
11.5. Tri topologique
inverse
Site Hosting: Bronco