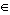[1,NbSommets],
La méthode de recherche en profondeur d'abord ("depth-first search") est la manière naturelle de parcourir un graphe, de visiter chaque sommet et d'emprunter chaque arc de manière systématique. De plus elle permet de répondre aux questions qui ont été soulevées en début de ce chapitre :
L'algorithme de recherche en profondeur se présente de la manière suivante : Comme son nom l'indique, l'on part d'un sommet et l'on essaie de s'éloigner le plus possible de ce sommet en cheminant le long des arcs. Si l'on rencontre un cul de sac (sommet n'ayant pas de voisin non encore visité), on revient en arrière et on repart en avant à la première occasion.
L'implantation de cette méthode que nous allons illustrer plus loin utilise un vecteur
NumeroDOrdre[i], i
qui indique, pour chaque sommet, avec quel numéro d'ordre il a été visité. Si NumeroDOrdre[j] = 0, cela indique que le sommet j n'a pas encore été visité.
Le programme suivant utilise une procédure récursive pour le parcours du graphe à partir d'un sommet donné; c'est la procédure "Visite". Visiter un sommet consiste à déterminer si, parmi les arcs qui y sont rattachés, il en existe qui mènent à des sommets pas encore visités. Si c'est le cas, l'on progresse le long d'un de ces arcs et, si cela n'aboutit pas, l'on progressera alors le long d'un autre de ces arcs.
procedure DFS( NbSommets: integer );
{ Algorithme de parcours d'un graphe en profondeur avec représentation
par liste de connectivité.
Les déclarations globales ainsi que la lecture du graphe sont
décrites au paragraphe 10.2.2 }
var CmptrVisite,
IndexSommet : 0..MaxNbSommets;
NumeroDOrdre: array[1..MaxNbSommets] of integer;
procedure Visite (IndexSommet : integer);
var Voisin : Ref;
begin
CmptrVisite := CmptrVisite + 1;
NumeroDOrdre[IndexSommet]:=CmptrVisite;
Voisin := PremierVoisin[IndexSommet];
while Voisin <> nil do begin
if NumeroDOrdre[Voisin^.IndexVoisin]=0 then
Visite (Voisin^.IndexVoisin);
Voisin := Voisin^.Suivant;
end; { while }
end; { Visite }
begin { DFS }
CmptrVisite := 0;
for IndexSommet:= 1 to NbSommets do
NumeroDOrdre[IndexSommet]:=0;
for IndexSommet := 1 to NbSommets do
if NumeroDOrdre[IndexSommet] = 0 then
Visite (IndexSommet)
end; { DFS }
La meilleure manière de suivre la progression de l'algorithme dans le parcours d'un graphe donné est de construire l'arbre des appels récursifs à la procédure Visite. On obtient ainsi un arbre unique ou une forêt dont chaque composante est appelée arbre de recherche en profondeur :
Les traits pleins dans cette figure indiquent que les sommets de niveau inférieur ont été trouvés par l'algorithme comme faisant partie de la liste de connectivité du sommet de niveau supérieur et n'avaient pas encore été visités; c'est donc par un appel récursif à la procédure Visite qu'il sont été atteints.
Les traits en pointillés correspondent à des arcs vers des sommets qui avaient déjà été visités; donc le test if ... then de la procédure Visite s'était révélé négatif et la récursivité s'était arrêtée là.
Pour un graphe représenté par une liste de connectivité, les structures de données produites sont :
IndexSommet 1 2 3 4 5 6 7 8 9 10 11 12 13
nom(IndexSommet) A B C D E F G H I J K L M
NumeroDOrdre[IndexSommet] 1 7 6 5 3 2 4 8 9 10 11 12 13
La complexité en temps de la procédure DFS, pour une représentation du graphe par liste de connectivité, est proportionnelle à NbSommets + NbArcs.
Si le graphe est représenté par une matrice de connectivité, on obtient un algorithme similaire où seule la procédure Visite a changé pour tenir compte de la différence de structure de donnée utilisée. Cet algorithme se présente de la manière suivante :
procedure DFS( NbSommets: integer );
{ Algorithme de parcours en profondeur d'un graphe non-orienté
avec représentation par matrice de connectivité.
Les déclarations globales ainsi que la lecture du graphe sont
décrites au paragraphe 10.2.1 }
var CmptrVisite,
IndexSommet : 0..MaxNbSommets;
NumeroDOrdre: array[1..MaxNbSommets] of integer;
procedure Visite (IndexSommet : integer);
var AutreSommet : integer;
begin
CmptrVisite := CmptrVisite + 1;
NumeroDOrdre[IndexSommet]:=CmptrVisite;
for AutreSommet := 1 to NbSommets do
if Relie[IndexSommet,AutreSommet] and
{ la condition qui suit permet d'éviter de boucler au cas où
il y aurait un cycle dans le graphe ou, tout simplement pour
éviter d'utiliser à nouveau un arc déjà parcouru en sens inverse }
(NumeroDOrdre[AutreSommet]=0) then
Visite (AutreSommet);
end; { Visite }
begin { DFS }
CmptrVisite := 0;
for IndexSommet:= 1 to NbSommets do
NumeroDOrdre[IndexSommet]:=0;
for IndexSommet := 1 to NbSommets do
if NumeroDOrdre[IndexSommet] = 0 then
Visite (IndexSommet)
end; { DFS }
La forêt de parcours que l'on obtient avec cet algorithme est légèrement différente de celle obtenue pour les listes de connectivité puisque les arcs partant d'un même sommet sont éventuellement traités dans un ordre différent.
La complexité en temps des DFS pour une représentation par matrice de connectivité est alors :
),
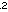ce qui confirme le choix intuitif qui avait été conseillé pour la matrice pour des graphes denses dans la mesure où la complexité en temps est indépendante du nombre d'arcs.
Un graphe a peut-être un cycle si l'on découvre dans la procédure "Visite" une composante non nulle dans le tableau NumeroDOrdre. Il faut donc pouvoir faire la distinction entre un cycle (par exemple A-B-C-D-A) et le parcours en sens inverse d'un arc déjà traité (par exemple A-B-A). Pour cela, il suffit de fournir un paramètre supplémentaire à la procédure Visite indiquant l'index du sommet précédant le sommet courant. Cela donne la variante suivante :
procedure DFS( NbSommets: integer );
{ Algorithme de parcours en profondeur d'un graphe non-orienté
avec représentation par liste de connectivité.
Version modifiée pour détecter les cycles. }
var CmptrVisite,
IndexSommet : 0..MaxNbSommets;
NumeroDOrdre: array[1..MaxNbSommets] of integer;
procedure Visite (IndexSommet,
Precedent : integer);
var Voisin : Ref;
begin
CmptrVisite := CmptrVisite + 1;
NumeroDOrdre[IndexSommet]:=CmptrVisite;
Voisin := PremierVoisin[IndexSommet];
while Voisin <> nil do
with Voisin^ do begin
if NumeroDOrdre[IndexVoisin]=0 then
Visite(IndexVoisin,IndexSommet)
else if IndexVoisin<>Precedent then (* cycle détecté *);
Voisin := Suivant;
end; { whith }
end; { Visite }
begin { DFS }
CmptrVisite := 0;
for IndexSommet:= 1 to NbSommets do
NumeroDOrdre[IndexSommet]:=0;
for IndexSommet := 1 to NbSommets do
if NumeroDOrdre[IndexSommet] = 0 then
Visite (IndexSommet,0)
end; { DFS }
Dans les deux algorithmes de parcours en profondeur vus au paragraphe 3 (pour les deux principales représentations d'un graphe), chaque appel non récursif à la procédure "Visite" détermine une nouvelle composante connexe du graphe. Nous allons voir ici une variante de l'algorithme DFS qui énumère, pour chaque sommet du graphe, les sommets vers lesquels il existe un chemin, c'est-à-dire la composante connexe dont il fait partie :
procedure SommetsAccessibles(NbSommets: integer);
{ cette procédure énumère, pour chaque sommet du graphe,
les sommets vers lesquels il existe un chemin }
var IndexSommet,
j : 0..MaxNbSommets;
AVisiter : array[1..MaxNbSommets] of boolean;
procedure Visite (IndexSommet : integer);
{ cette procédure va parcourir toute une composante connexe }
var AutreSommet : integer;
begin
AVisiter[IndexSommet] := false;
write(Nom(IndexSommet));
for AutreSommet :=1 to NbSommets do
if Relie[IndexSommet,AutreSommet] and AVisiter[AutreSommet] then
Visite (AutreSommet);
end; { Visite }
begin { SommetsAccessibles }
for IndexSommet:=1 to NbSommets do begin
for j := 1 to NbSommets do AVisiter[j] := true;
Visite (IndexSommet)
writeln;
end; { for }
end; { SommetsAccessibles }
10.4. Recherche
en largeur
Site Hosting: Bronco
Table des
matières.