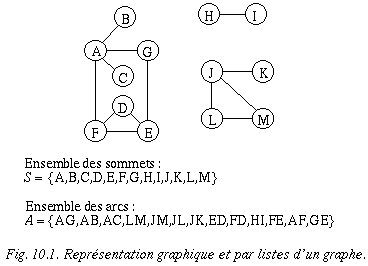
Un graphe est une collection de sommets et d'arcs. Un sommet est un objet simple qui peut avoir un nom et d'autres propriétés. Un arc est une connexion entre deux sommets. Il existe plusieurs manières de représenter les graphes. Entre autres, sous forme graphique ou sous forme de listes de sommets et d'arcs. La représentation graphique d'un graphe n'est toutefois utilisable que par un humain et uniquement si le graphe est peu dense ou contient relativement peu de sommets. La figure 10.1 ci-dessous en illustre un exemple :
Un chemin du sommet x au sommet y est une liste de sommets dans laquelle chaque sommet successif est relié au précédent par un arc.
Un graphe est connexe s'il existe un chemin de chaque sommet vers chaque autre sommet; sinon, il est formé de composantes connexes.
Un chemin simple est un chemin dans lequel aucun arc n'est répété.
Un cycle est un chemin simple ayant le même sommet aux deux extrémités. Il est à noter que dans l'exemple ci-dessus, le chemin AGA n'est pas considéré comme un cycle puisque ce n'est pas un chemin simple.
Si un graphe, à S sommets, a moins de S-1 arcs il ne peut pas être connexe; s'il a plus de S-1 arcs, il doit avoir un cycle.
Les graphes tels que définis jusqu'ici sont des graphes non-orientés. Un graphe est orienté si on associe un sens unique à chaque arc.
Un graphe est pondéré si, à chaque arc, on associe une valeur représentant par exemple une distance, un coût, un débit, etc. Les graphes orientés et pondérés sont appelés des réseaux.
Description en terme de types abstraits :
 10.2.
Représentation
10.2.
Représentation
Site Hosting: Bronco