Il est possible de représenter des listes à l'aide de structures d'arbres et vice-versa. Les deux structures ont en effet des caractéristiques suffisamment proches pour cela. Cela n'a bien entendu d'intérêt que si l'une de ces deux structures est privilégiée par le langage de programmation utilisé.
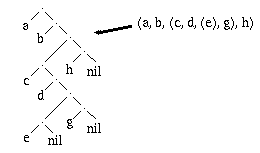
Pour représenter une liste sous forme d'arbre, on utilise généralement une structure d'arbre binaire dont les noeuds non-terminaux ne comportent pas d'informations particulières. La transformation que l'on peut adopter sera de mettre le premier élément de la liste (car) comme sous-arbre gauche de la racine et le reste de la liste (cdr) comme sous-arbre droit de la racine. Le processus est réitéré pour chaque morceau de liste qui reste. Un atome de la liste deviendra une feuille de l'arbre et une sous-liste deviendra un sous-arbre droit (algorithme récursif).
Exemple
Fig. 9.4. Transformation d'une liste en arbre binaire.
Il serait possible de représenter une liste sous forme d'arbre multiple. Toutefois, comme on l'a vu au chapitre sur les structures d'arbre, il est difficile de représenter un arbre multiple dont on ne connaît pas par avance le degré.
Pour représenter un arbre multiple sous forme de liste, on peut adopter la convention selon laquelle le contenu du noeud racine est mis en première position de la liste et chacun de ses sous-arbres constituera une sous-liste de la liste principale (algorithme récursif).
Exemple
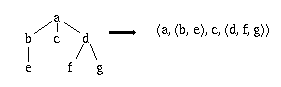
Fig. 9.5. Transformation d'un arbre multiple en liste.
Pour représenter un arbre binaire ordonné sous forme de liste, on peut d'une manière similaire adopter la convention selon laquelle le contenu du noeud racine est mis en première position de la liste et chacun de ses sous-arbres constituera une sous-liste de la liste principale (algorithme récursif). Si un sous-arbre est inexistant, on lui fera correspondre une liste vide.
Exemple
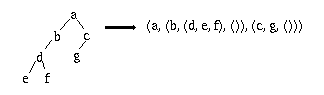
Fig. 9.6. Transformation d'un arbre binaire en liste.
10. Structures
récursives non linéaires : les graphes
Site Hosting: Bronco
Table des
matières.