Pour les langages n'offrant pas la possibilité de faire de l'allocation dynamique, c'est la structure de tableau qui est généralement employée en remplacement. Les pointeurs vers des éléments sont alors remplacés par des indices dans le tableau :
const TailleMax = ...;
INil = 0;
type VersElement = 0..TailleMax;
Element = record
Info: ...;
Gauche,
Droit: VersElement;
end; { Element }
var Elements : array [1..TailleMax]
of Element;
Racine : VersElement;
Il arrive souvent (pour les arbres de tri, par exemple) que la racine corresponde systématiquement à la première position du tableau. Dans ces cas, il arrive que l'on omette d'utiliser explicitement un pointeur racine. Il serait toutefois plus élégant de déclarer Racine comme une constante valant 1.
Si l'on examine l'algorithme de parcours d'une structure d'arbre, on peut se rendre compte qu'il est indispensable d'utiliser une structure de pile pour pouvoir effectuer le parcours. Si l'on utilise un langage offrant la récursivité, c'est la pile d'activation des procédures, gérée par le système, qui est utilisée. Si l'on emploie un langage de programmation n'offrant pas la récursivité, c'est à l'utilisateur de gérer explicitement une pile des ancêtres mis en attente pour traiter leurs sous-arbres gauches. Cela peut être fait de la manière suivante (il faut déclarer une structure de pile en plus des déclarations vues plus haut) :
type PileDef = record
Sommet: 0..TailleMax;
Contenu: array [1..TailleMax]
of VersElement;
end; { PileDef }
var Pile: PileDef;
{ Pour la définition des primitives de
manipulation de piles, se rapporter à
la section 6.3.1. du chap. précéd. }
procedure ParcoursNonRecursif(
Racine: VersElement);
var Courant: VersElement;
begin { ParcoursNonRecursif }
Courant := Racine;
while (Courant <> INil) or
not Vide(pile) do begin
if Courant=INil then Pop(Pile,Courant)
else while Elements[Courant].Gauche
<> INil do begin
Push(Courant,Pile);
Courant:= Elements[Courant].Gauche;
end; { while Elements... }
Traite(Courant);
Courant := Elements[Courant].Droit;
end; { while }
end; { ParcoursNonRecursif }
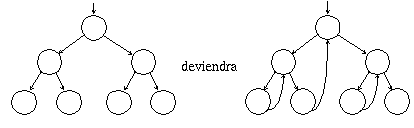
Plutôt que d'utiliser une structure de pile pour retrouver les ancêtres, lors du parcours en ordre d'un arbre représenté à l'aide d'un tableau, on peut tirer profit de ce que le pointeur Droit de l'élément le plus à droite d'un sous-arbre gauche est inutilisé pour le faire pointer vers l'ancêtre immédiat de la racine de ce sous-arbre.
Exemple

Fig. 8.8. Ajout d'arcs "ancêtre"
L'intérêt d'une telle structure est de permettre l'utilisation d'un algorithme de parcours ne nécessitant l'utilisation ni d'une pile ni de la récursivité. L'utilisation mémoire d'un tel algorithme sera donc plus réduite que les algorithmes de parcours d'arbres "normaux".
Le parcours d'une telle structure ne peut toutefois pas se faire sans précaution. On peut en effet remarquer que les pointeurs qui ont été rajoutés font apparaître des boucles dans la structure. Il faut donc s'assurer, lorsque l'on suit un pointeur gauche qui mène à un sous-arbre, que l'on n'utilisera pas ce même pointeur gauche à nouveau quand le dernier pointeur Droit du sous-arbre nous aura ramené vers l'ancêtre immédiat.
De prime abord, on pourrait envisager de "casser" le pointeur gauche (le mettre à nil) après l'avoir utilisé, afin d'être sûr de ne pas l'utiliser à nouveau. Cela aurait toutefois le désavantage de modifier la structure lors du parcours et, par conséquent, de ne permettre qu'un seul parcours.
Le fait que l'on utilise des nombres entiers en guise de pointeur nous permet d'envisager une autre solution relativement simple. Cette solution consiste à changer le signe du pointeur gauche que l'on vient d'utiliser et d'ignorer, ensuite, tout pointeur négatif. A la fin du parcours, il ne reste plus qu'à remettre tous les pointeurs du tableau à des valeurs positives pour retrouver la structure d'origine. Ces différentes manipulations peuvent se faire à l'aide des algorithmes suivants :
program ArbreDepliable;
const TailleMax = ...;
Racine = 1;
PseudoNil = 0;
type Information = ...;
Noeud = record
Info: Information;
Gauche, Droit: integer;
end; { Noeud}
var Noeuds: array[1..TailleMax] of Noeud;
Libre: 1..TailleMax;
Insere: boolean;
Valeur: Information;
procedure InsereGauche(Valeur: Information;
Parent: integer);
{ Cette procédure insère un nouvel
élément juste à gauche de l'élément
"Parent" dont la position est passée
en paramètre.
La valeur de ce nouvel élément est
passé en paramètre à la procédure.
La structure est mise à jour par effet
de bord.
La procédure met aussi à TRUE la
variable globale "Insere" qui est
utilisée dans la procédure "Ajout". }
begin { InsereGauche }
with Noeuds[Libre] do begin
Info := Valeur;
Gauche := PseudoNil;
Droit := Parent;
end; { with }
Noeuds[Parent].Gauche := Libre;
Libre := succ(Libre);
Insere := true;
end; { InsereGauche }
procedure InsereDroite(Valeur: Information;
Parent: integer);
{ Cette procédure insère un nouvel
élément juste à droite de l'élément
"Parent" dont la position est passée
en paramètre.
La valeur de ce nouvel élément est
passé en paramètre à la procédure.
La structure est mise à jour par effet
de bord.
La procédure met aussi à TRUE la
variable globale "Insere" qui est
utilisée dans la procédure "Ajout".}
begin { InsereDroite }
with Noeuds[Libre] do begin
Info := Valeur;
Gauche := PseudoNil;
Droit := Noeuds[Parent].Droit;
end; { with }
Noeuds[Parent].Droit := Libre;
Libre := succ(Libre);
Insere := true;
end; { InsereDroite }
procedure Ajout(Valeur: Information);
{ Cette procédure ajoute un nouvel
élément dans la structure.
La valeur de ce nouvel élément est
passé en paramètre à laprocédure.
La structure est mise à jour par effet
de bord.Cette procédure utilise la variable
globale "Insere" qui est modifiée par
effet de bord dans les procédures
"InsereGauche" et "InsereDroite" pour
indiquer que le nouvel élément a
été placé. }
var Courant: 1..TailleMax;
begin { Ajout }
Courant := Racine;
Insere := false;
repeat
with Noeuds[Courant] do
{ faut-il aller àdroite? }
if Info < Valeur then
{ élém.à droite pas ancêtre? }
if Droit >Courant then
{ si oui, on va à droite }
Courant := Droit
else
{sinon insère nouveau }
InsereDroite(Valeur, Courant)
{ y a-t-il un descendant à gauche?}
else if Gauche<> PseudoNil then
{ si oui, on va à gauche }
Courant := Gauche
else InsereGauche(Valeur, Courant);
until Insere;
end; { Ajout }
procedure Parcours;
var Courant, Temp: PseudoNil..TailleMax;
begin
Courant := Racine;
{ boucle de parcours des noeuds }
repeat
{ va le plus à gauche possible }
while Noeuds[Courant].Gauche>
PseudoNil do
{ après chaque déplacement à
gauche, on "casse" le pointeur utilisé }
with Noeuds[Courant] do begin
Courant := Gauche;
Gauche := -Gauche;
end ;{ while-with }
Traite(Courant);
{ La procédure Traite pourrait, par
exemple, correspondre à :
writeln(Noeuds[Courant].Valeur) }
Courant := Noeuds[Courant].Droit;
until Courant = PseudoNil;
{ remise en état des pointeurs Gauche }
for Courant := 1 to pred(Libre) do
with Noeuds[Courant] do
if Gauche < PseudoNil then
Gauche := -Gauche;
end; { Parcours }
begin { ArbreDepliable }
{ on lit le premier élémentséparément}
with Noeuds[Racine] do begin
Lire(Info); {on suppose que cette pro-
cédure lit une valeur }
Gauche := PseudoNil;
Droit := PseudoNil;
end; { with }
Libre := 2;
{ lecture+insertion desélém. suivants}
while not eof(input) do begin
Lire(Valeur);
Ajout(Valeur);
end; { while}
Parcours;
end. { ArbreDepliable }
 8.4.
Rééquilibrage d'arbres
8.4.
Rééquilibrage d'arbres
Site Hosting: Bronco