Parmi les différentes structures d'arbres possibles, une des plus intéressantes à utiliser est la structure d'arbre binaire ordonné (arbre de tri, arbre syntaxique, arbre généalogique...).
Exemple
type Noeud = record
Info : InfoType;
Gauche, Droite : ^Noeud;
end; { Noeud }
var Racine : ^Noeud;
{initialisation:}Racine:=nil;{arbre vide}
Description en terme de type abstrait :
Les primitives 3,9,10 et 11 peuvent être combinées pour supprimer un élément quelconque d'un arbre.
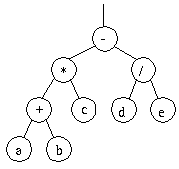
Un arbre syntaxique est une structure chargée de refléter la précédence existant entre les différents opérateurs et symboles d'un langage. Ils sont souvent utilisés pour représenter des expressions algébriques. Dans ce cas, chaque noeud intérieur contient un opérateur et les feuilles contiennent les opérandes. La hiérarchie des sous-arbres reflète la précédence des opérateurs et des parenthèses.
type Genres = (Operateur, Constante,
Variable);
VersNoeud = ^Noeud;
Noeud = record
Gauche,Droite: VersNoeud;
case Genre: Genres of
Operateur,
Variable : (Car: char);
Constante : (Valeur: integer);
end; { Noeud }
var Racine : VersNoeud;
Exemple : (a+b)*c-d/e

Fig.8.2. Arbre syntaxique d'une expression arithmétique.
La construction d'un arbre syntaxique se fait souvent en combinant un élément (opérateur) et deux arbres (opérandes) pour former un nouvel arbre.
Un arbre de tri est une structure chargée de refléter une relation d'ordre existant entre différentes informations. Ces informations doivent comporter un champ (clé de tri) sur lequel on puisse appliquer une fonction permettant de savoir si un élément doit être avant ou après un autre. La plupart du temps, ce champ sera de type numérique ou alphabétique sur lequel on pourra utiliser les opérateurs de comparaison: <, > ou =. Un arbre de tri reflète un séquencement (linéaire) des éléments qu'il contient. Le même ensemble de valeurs peut donc être représenté par différentes configurations d'arbres binaires suivant l'ordre selon lequel les valeurs auront été traitées.
Exemple
type VersNoeud = ^Noeud;
Noeud = record
Cle: integer;
Petits, Grands: VersNoeud;
end; { Noeud }
var Racine: VersNoeud; i: integer;
procedure Insere(Valeur: integer;
var P: VersNoeud);
begin { Insere }
if P = nil then begin
new(P);
with P^ do begin
Cle := Valeur;
Petits := nil;
Grands := nil;
end; { with }
end { then }
else if Valeur < P^.Cle then
Insere(Valeur, P^.Petits)
else if Valeur > P^.Cle then
Insere(Valeur, P^.Grands);
end; { Insere }
procedure Imprime(P: VersNoeud);
begin { Imprime }
if P^.Petits <> nil then
Imprime(P^.Petits);
writeln(P^.Cle);
if P^.Grands <> nil then
Imprime(P^.Grands);
end; { Imprime }
begin { programme }
Racine := nil; { arbre vide }
while not eof(input) do begin
{ construction }
read(i);
Insere(i,Racine);
end; { while }
Imprime(Racine); { parcours }
end.
Les opérations les plus courantes que l'on effectue sur une structure
d'arbre sont les suivantes :
Il est bien entendu possible d'effectuer bien d'autres opérations sur des arbres. Par exemple combiner 2 arbres, extraire un sous-arbre d'un arbre, etc... Ces opérations dépendent étroitement du problème qu'elles sont sensées résoudre et nous n'en donnerons pas d'exemple ici.
Comme on a pu le voir précédemment, dans un arbre de tri, un élément est toujours inséré en position terminale (feuille).
La suppression d'un noeud pose généralement plus de problèmes
que l'insertion. Pour un arbre de tri, il faut distinguer trois cas :
La suppression d'une feuille ne pose pas de problème; il suffit de mettre à nil le pointeur vers l'élément à détruire et de récupérer la place occupée par l'élément détruit.
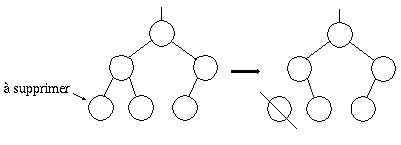
Fig. 8.3. Suppression d'une feuille
La suppression d'un noeud n'ayant qu'un seul descendant est à peine plus compliquée. Il suffit de faire pointer l'ancêtre directement vers le descendant.
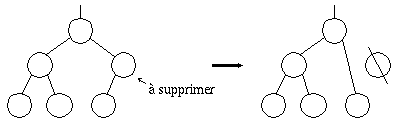
Fig. 8.4. Suppression d'un noeud à un seul descendant.
La suppression d'un noeud ayant deux descendants est plus délicate. Il faut d'abord trouver l'élément le plus à droite du sous-arbre gauche (le plus grand élément inférieur à celui que l'on veut détruire); ce sera une feuille ou un noeud à un seul descendant gauche. On transfère alors le contenu de la feuille (ou du noeud à un seul descendant gauche) dans le noeud que l'on voulait détruire et l'on détruit la feuille (ou le noeud à un seul descendant gauche) à la place.
Le cas où l'élément le plus à droite du sous-arbre gauche est une feuille est illustré à la figure 8.5, alors que celui où l'élément le plus à droite du sous-arbre gauche est un noeud à un seul descendant est illustré à la figure 8.6.
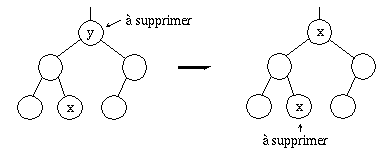
Fig. 8.5. Suppression d'un noeud à deux descendant, échange avec une feuille.
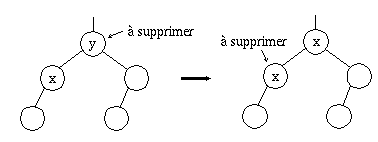
Fig. 8.6. Suppression d'un noeud à 2 descendants, échange avec un noeud à un descendant.
On peut compléter l'algorithme du paragraphe 1.2. pour ajouter une procédure de suppression d'élément comme suit :
procedure Supprime(var P: VersNoeud);
var T1,T2: VersNoeud;
begin { Supprime }
if (P^.Petits=nil) and
(P^.Grands=nil) then
dispose(P) { une feuille }
else if P^.Petits=nil then begin
T1 := P; { 1 seul descendant }
P := P^.Grands;
dispose(T1);
end
else if P^.Grands=nil then begin
T1 := P; { 1 seul descendant }
P := P^.Petits
dispose(T1);
end
else begin { 2 descendants }
T1 := P^.Petits;
{ dans le sous-arbre des éléments
plus petits, y a-t-il des éléments
plus grands que la racine locale?
Dans la négative, échanger puis
supprimer la racine locale }
if T1^.Grands = nil then begin
P^.Cle := T1^.Cle;
Supprime(P^.Petits);
end
else begin
{ recherche du plus grand élément
du sous-arbre gauche }
while T1^.Grands <> nil do begin
T2 := T1;
T1 := T1^.Grands;
end; { while }
{ à la fin de la boucle, T1 pointe
vers le plus grand des éléments
du sous-arbre et T2 vers son
ancêtre immédiat }
P^.Cle := T1^.Cle;
Supprime(T2^.Grands);
end;
end; { 2 descendants }
end; { Supprime }
La recherche d'un élément dans un arbre de tri est très similaire à l'insertion telle que nous l'avons vue en 8.1.2. Nous verrons donc ici une variante non récursive :
procedure Recherche( Racine: VersNoeud;
Valeur: integer;
var Emplacement: VersNoeud);
{ Si la valeur recherchée ne se trouve
pas dans l'arbre, Emplacement sera mis à nil. }
begin { Recherche }
Emplacement := Racine;
while (Emplacement <> nil) and
{$R-} (* suppression contrôle *)
(Emplacement^.Cle <> Valeur)
{$R^} do
if Emplacement^.Cle > Valeur then
Emplacement:=Emplacement^.Petits
else
Emplacement:=Emplacement^.Grands;
end; { Recherche }
On parcourt généralement un arbre pour appliquer un traitement
à chacun de ses noeuds. On distingue plus particulièrement
trois méthodes de parcours d'arbres binaires :
en pré-ordre : on traite la racine puis le sous-arbre gauche et enfin le sous-arbre droit.
en ordre : on traite le sous-arbre gauche puis la racine et enfin le sous-arbre droit.
en post-ordre : on traite le sous-arbre gauche puis le sous-arbre droit et enfin la racine.
L'impression d'un arbre de tri se fait à l'aide d'un parcours en ordre puisque la valeur stockée dans le noeud racine se situe entre les valeurs du sous-arbre gauche et celles du sous-arbre droit. L'évaluation d'un arbre syntaxique se fait avec un parcours en post-ordre puisqu'il faut évaluer les deux opérandes avant de pouvoir traiter l'opérateur. A titre d'exemple, le parcours en ordre d'un arbre binaire peut se faire de la manière suivante :
procedure ParcoursEnOrdre(Racine: VersElement);
begin { ParcoursEnOrdre }
if Racine^.Gauche <> nil then
ParcoursEnOrdre(Racine^.Gauche);
Traite(Racine);
if Racine^.Droite <> nil then
ParcoursEnOrdre(Racine^.Droite);
end; { ParcoursEnOrdre }
 8.2. Arbres multiples
8.2. Arbres multiples
Site Hosting: Bronco