Ces structures de données que l'on qualifie aussi de structures intermédiaires car elles s'utilisent souvent en conjonction avec d'autres, sont d'une grande importance dans de nombreux domaines tels que :
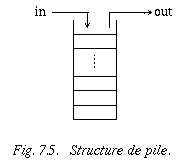
Ces structures se caractérisent par un comportement particulier en ce qui concerne l'insertion et l'extraction d'un élément. Ainsi, pour une pile, on insère et on extrait les éléments à la même extrémité de la suite linéaire. Pour la file d'attente, l'insertion se fait à un bout et l'extraction à l'autre.
Les piles ont la propriété que le dernier élément inséré est le premier à pouvoir en être extrait. On utilise souvent le terme de LIFO (de l'anglais "Last In First Out") Exemple d'utilisation Traitement des structures emboîtées (par exemple, analyse d'un programme : boucles imbriquées, procédures locales; parcours d'arbres, etc.) pour lesquelles il faut que les sous-structures soient traitées avant la structure qui les contient. Si on traite une structure de niveau "n" et que l'on rencontre une sous-structure S, on interrompt le traitement au niveau "n" en plaçant les informations indispensables sur la pile qui nous permettront de reprendre le traitement de "n" après avoir terminé celui de S. Ainsi à tout moment la pile contient, dans l'ordre inverse, les informations relatives aux niveaux momentanément interrompus.
Description en terme de type abstrait :
Si l'on compare cette description avec celle qui a été faite au début de ce chapitre concernant les chaînes, on peut facilement se convaincre qu'une structure de chaîne peut être utilisée pour implanter une structure de pile. Il suffit en effet de se restreindre à des manipulations en début de chaîne (insertion, suppression, accès) pour respecter les contraintes de la structure de pile.
Une file d'attente est caractérisée par le fait que les insertions se font à un bout de la suite et les extractions à l'autre. En anglais, on parle de FIFO (First In First Out).
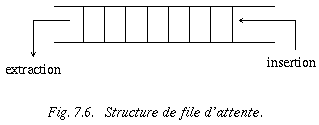
Dans une file d'attente l'ordre d'arrivée des éléments est préservé.
Exemples d'utilisation
Description en terme de type abstrait :
Comme pour les piles, la comparaison de la description qui précède avec celle des chaînes nous montre qu'une file d'attente peut être implantée à l'aide d'une structure de chaîne. Du fait que l'on a besoin d'accéder aux deux extrémités de la structure (en début pour la suppression et en fin pour l'insertion), il faut gérer la chaîne avec un pointeur Début et un pointeur Fin, ou alors utiliser un anneau.
Notation
Indépendamment de la représentation et de l'implantation d'une structure de pile ou de file d'attente, on peut exprimer les actions d'insertion et d'extraction comme :
Px insérer l'élément x dans la pile P
x
F
x
Exemple
si F est une file d'attente initialement vide, F = ( )
si F
si F
si F
si x
Si P est une pile dont les éléments sont des paires de valeurs numériques entières ordonnées :
si P
si P
si xx est une variable structurée.
Il y a plusieurs manières de représenter les piles et les files d'attente. Entre autres la représentation séquentielle (par tableaux) et la représentation chaînée (par pointeurs). Etant donné que nous avons déjà pas mal détaillé les algorithmes de gestion de chaînes, nous nous contenterons ici de voir la représentation par tableau. L'implantation à l'aide de tableaux impose une contrainte supplémentaire par rapport à ce qui peut être réalisé à l'aide de chaînes. Cette contrainte consiste à imposer un quota maximum au nombre d'éléments qui peuvent être stockés dans la structure, ceci à cause de la nature statique de la structure de tableau.
const Max=...; {hauteur max. de la pile}
type Objet = ...;
Pile = record
Element : array [1..Max] of Objet;
Sommet : 0..Max;
end; { Pile }
var P : Pile;
P.Sommet := 0; {pile vide}
function Vide (P:Pile) : boolean;
begin
Vide := P.Sommet = 0;
end; { Vide }
procedure Pop (var P: Pile; var Valeur: Objet);
begin
if Vide (P) then Erreur ('pile vide')
else begin
Valeur := P.Element[P.Sommet];
P.Sommet := pred(P.Sommet);
end;
end; { Pop }
procedure Push(var P: Pile; Valeur: Objet);
begin
if P.Sommet = Max then Erreur('pile pleine')
else begin
P.Sommet := succ(P.Sommet);
P.Element [P.Sommet] := Valeur;
end;
end; { Push }
Comme nous allons pouvoir le remarquer, l'organisation la plus simple d'une file d'attente à l'intérieur d'un tableau n'est pas très efficace. C'est pourquoi une solution de file circulaire sera aussi proposée.
const Max = ...;
type Objet = ...;
FileDAttente = record
Element: array[1..Max] of Objet;
NbElements: 0..Max;
end; { FileDAttente }
var F: FileDAttente;
F.NbElements := 0;
function Vide (F: FileDAttente): boolean;
begin
Vide := F.NbElements=0;
end; { Vide }
procedure Ote(var F: FileDAttente; var Valeur: Objet);
var i: integer;
begin
if Vide(F) then Erreur('file vide')
else with F do begin
Valeur := Element[1];
for i := 2 to NbElements do
Element[pred(i)] := Element[i];
NbElements := pred(NbElements);
end; { with }
end; { Ote }
procedure Met(var F: FileDAttente; Valeur: Objet);
begin
with F do begin
if NbElements = Max then Erreur('file pleine')
else begin
NbElements := succ(NbElements);
Element[NbElements] := Valeur;
end; { else }
end; { with }
end; { Met }
const Max = ...;
type Objet = ...;
FileCirculaire = record
Element: array[0..Max] of Objet;
IndexIn,
IndexOut: 0..Max;
Plein:boolean;
end; { FileCirculaire }
var B: FileCirculaire;
B.IndexIn := 0; B.IndexOut := 0; B.Plein := false;
function Vide(B: FileCirculaire): boolean;
begin
with B do Vide := (IndexIn = IndexOut) and not Plein;
end; { Vide }
procedure Met( var B: FileCirculaire; Valeur: Objet);
begin
if B.Plein then Erreur('buffer plein')
else with B do begin
Element[IndexIn] := Valeur;
IndexIn:=succ(IndexIn) mod succ(Max);
Plein := IndexIn=IndexOut;
end; { with }
end; { Met }
procedure Ote( var B: FileCirculaire; var Valeur: Objet);
begin
with B do begin
if Vide(B) then Erreur('file vide')
else begin
Valeur := Element[IndexOut];
IndexOut := succ(IndexOut) mod succ(Max);
Plein := false;
end; { else }
end; { with }
end; { Ote }
8. Structures
récursives non linéaires : les arbres
Site Hosting: Bronco
Table des
matières.