7.4. Anneaux, chaînes bidirectionnelles

7.4.1. Les anneaux

 Si l'on revient un instant sur l'algorithme "InsertionFin2", on peut remarquer que, pour accélérer l'insertion en fin de chaîne, nous avons été amenés à ajouter un pointeur "fin de chaîne" en plus du pointeur "début". Une autre solution consiste à rendre la chaîne circulaire. Cela se fait en remplaçant, dans le dernier élément, le pointeur "Suivant" à nil par un pointeur "Suivant" qui pointe vers le premier élément de la liste. Il est alors plus simple d'avoir un pointeur "Dernier" en lieu et place du pointeur "Début" :

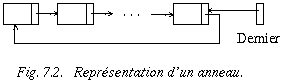
Une telle chaîne circulaire s'appelle un anneau. L'intérêt d'une telle structure est de pouvoir atteindre tous les éléments de la chaîne depuis n'importe quel élément. Nous pouvons alors considérer la chaîne comme n'ayant ni début ni fin. Si l'on désire toutefois pouvoir reconnaître le premier élément, il suffit de tester si le pointeur vers cet élément est égal au pointeur "Dernier^.Suivant".

7.4.1.1. Manipulations sur les anneaux

Les algorithmes d'insertion, de suppression et de parcours d'éléments sont très similaires à ceux que nous avons vus pour les chaînes linéaires. Il faut juste faire attention, lors d'insertion ou de suppression en fin, de mettre correctement à jour le pointeur dernier. De plus, lors d'insertion après un élément donné, il faut tester si l'insertion s'est faite en fin d'anneau pour ajuster le pointeur Dernier en conséquence. Pour une insertion avant un élément donné, il faut renoncer au "truc" de l'insertion "après" avec échange des contenus, si l'élément donné se trouve en fin de chaîne.

La plupart des algorithmes d'insertion doivent traiter le cas particulier de l'anneau vide. Cela peut se faire à l'aide des instructions suivantes : 

  if Dernier = nil then begin {anneau vide}
    new(Dernier);
    with Dernier^ do begin
      Info := ...;
      { l'él. est son propre succ.}
      Suivant := Dernier;
      end; { with }
    end; { if }
Pour le parcours d'un anneau il faut prendre en compte le fait qu'il n'y a plus de pointeur à nil pour indiquer la fin de la chaîne. Cela donne un algorithme de parcours tel que : 
  procedure Parcours(dernier: VersElement;
                     Traite: procedure);

  var Courant, premier: VersElement;

  begin { Parcours }
    if Dernier = nil then { anneau vide }
    else begin
      Premier := Dernier^.Suivant;
      Courant:= Premier;
      repeat
        { traitement quelconque à
          appliquer à chaque élément }
        Traite(Courant);
        Courant := Courant^.Suivant;
      until Courant = Premier;
    end;
  end; { Parcours }

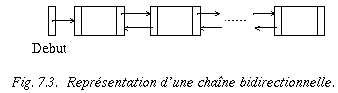
7.4.2. Les chaînes bidirectionnelles

 Si l'on désire souvent pouvoir atteindre des éléments d'une chaîne qui se trouvent quelques positions avant un élément donné, on peut alors adjoindre, à chaque élément, un pointeur supplémentaire vers son prédécesseur. On obtient alors une chaîne bidirectionnelle :

La déclaration contient un pointeur supplémentaire chargé d'indiquer l'emplacement du prédécesseur. Il faut donc que, lors de l'insertion ou de la suppression d'un élément, l'on tienne à jour les deux pointeurs des éléments impliqués dans l'opération.

7.4.2.1. Manipulations sur les chaînes bidirectionnelles

Exemple d'insertion en début (ressemble beaucoup à l'exemple vu au paragraphe 1) : 
  type VersElement = ^Element;
       Element = record
                   Info: ...;
                   Precedent,
                   Suivant : VersElement;
                   end; { Element }

  procedure InsertionDebut(var Debut: VersElement;
                               Information: ...);

  var Nouveau: VersElement;

  begin { InsertionDebut }
    new(Nouveau);
    with Nouveau^ do begin
      Info := Information;
      Suivant := Debut;
      Precedent := nil;
      end; { with }
    if Debut <> nil then Debut^.Precedent := Nouveau;
    Debut := Nouveau;
  end; { InsertionDebut }
Exemple d'insertion avant un élément donné (il n'est plus nécessaire d'utiliser le "truc" de l'insertion après avec échange des contenus) : 
  procedure InsertionAvant(var Debut: VersElement;
                               Courant: VersElement;
                               Information: ...);
  var Nouveau: VersElement;

  begin { InsertionAvant }
    { création d'un nouvel élément }
    new(Nouveau);
    with Nouveau^ do begin
      Info := Information;
      Suivant := Courant;
      Precedent := Courant^.Precedent;
      end; { with }

    { modification des liens des éléments existants }
    Courant^.Precedent := Nouveau;
    if Debut = Courant then Debut := Nouveau
    else Nouveau^.Precedent^.Suivant := Nouveau;
  end; { InsertionAvant }
Exemple de suppression d'un élément donné : 
  procedure SuppressionMilieu(var Debut: VersElement;
                              var Courant: VersElement);

  begin { SuppressionMilieu }
    { mise-à-jour du pointeur Suivant du
      prédécesseur et du pointeur Precedent
      du successeur }
    if Courant = Debut then begin
      Debut := Debut^.Suivant;
      if Debut <> nil then
        Debut^.Precedent := nil;
      end
    else with Courant^ do begin
      Precedent^.Suivant := Suivant;
      if Suivant <> nil then
        Suivant^.Precedent := Precedent;
      end; { with }
    { destruction de l'élément courant }
    dispose(Courant);
  end; { SuppressionMilieu }
Pour une chaîne bidirectionnelle, l'insertion ou la suppression en fin implique toujours un parcours complet de la chaîne depuis son début, à moins que, comme pour les chaînes monodirectionnelles, l'on gère un pointeur Fin.

7.4.3. Les anneaux bidirectionnels

 Une chaîne bidirectionnelle peut, elle aussi, être rendue circulaire. On obtient alors un anneau bidirectionnel :

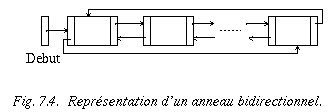
Cette structure bénéficie des avantages combinés qu'apportent le pointeur "Prédécesseur" et la circularité. Les opérations de suppression d'éléments et les manipulations en fin de chaîne s'en trouvent nettement simplifiées.

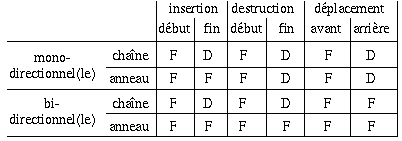
On peut d'ailleurs résumer la facilité avec laquelle on peut effectuer les opérations d'insertion, de destruction et de déplacement dans une chaîne, ou dans les différentes variantes que l'on vient de voir, de la manière suivante (F=facile, D=difficile) :

7.5. Utilisation d'un élément sans données

Table des matières.