S1 : T1; S2 : T2; Sn : Tn;
end;
composantes:
et le calcul de l'indice
déclaré d'un élément
avec l'opérateur de relation in
composantes:
de type To
différents
type scalaire To
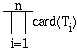
prod.cartésie
Définition : La cardinalité est le nombre de valeurs distinctes appartenant à un type T. Un objet de ce type T ne pourra bien entendu avoir qu'une seule de ces valeurs à un instant donné
Exemple
type Forme = (Carré, Rectangle, Cercle,
Ellipse);
Monnaie = (Franc, Livre, Dollar,
Lire, Yen, Mark);
Genre = (Feminin, Masculin);
card(Forme) = 4
card(Monnaie) = 6
card(Genre) = 2
type SmallInteger = 1..100;
type Vecteur=array[1..3] of SmallInteger;
card (SmallInteger) = 100
card (Vecteur) = 1003
card (boolean) = 2
card (integer) = 2*(MaxInt+1) { pour le langage Pascal
}
card (real) = 2n-1 pour une représentation normalisée,
où n est le nombre de bits utilisés pour représenter
les nombres réels. Le premier bit de la mantisse étant toujours
à 1, sauf pour la valeur 0.0, certaines architectures ne mémorisent
pas ce premier bit et ont, par conséquent, une cardinalité
de 2n pour les nombres réels.
On peut résumer les principales caractéristiques des structures cartésiennes simples dans le tableau suivant :
| Structure : | Tableau | Enregistrement | Ensemble |
| Déclaration | a : array[I] of To | r : record S1 : T1; S2 : T2; Sn : Tn; end; |
set of To |
| Sélecteur : | a[i] (i |
r.s (S |
aucun |
| Accès aux composantes: |
par le sélecteur et le calcul de l'indice |
par le sélecteur avec le nom déclaré d'un élément |
Test d'appartenance avec l'opérateur de relation in |
| Type des composantes: |
Toutes ident. de type To |
Peuvent être différents |
Toutes ident. et de type scalaire To |
| Cardinalité : | Card(To)Card(I | 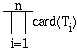 prod.cartésie |
2Card(TO) |
Ces structures simples peuvent être combinées pour former des structures plus complexes .
 3.3. Structures
cartésiennes complexes
3.3. Structures
cartésiennes complexes
Site Hosting: Bronco