2.3. Les réels

De tous les types de base, ce sont les nombres réels qui posent le plus de problèmes de représentation. L'ensemble des nombres réels étant, par définition, infini et indénombrable, il est impossible de le représenter avec une totale exactitude dans un ordinateur. La représentation qui en est faite ne peut donc constituer qu'une approximation. Il existe d'ailleurs plusieurs techniques de représentation, chacune ayant ses avantages et ses inconvénients.

2.3.1. Représentation en virgule flottante

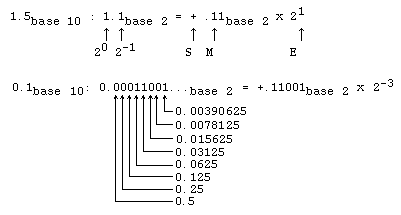
La représentation en virgule flottante consiste à représenter un nombre réel à l'aide de 3 composantes : le signe (S), l'exposant (E) et la mantisse (M). L'on considère que la virgule décimale est placée juste à gauche de la mantisse et que le bit de poids le plus élevé de la mantisse est à 1 (sauf pour représenter 0.0), de façon que la mantisse représente toujours un nombre compris dans l'intervalle [0.5,1.0] (valeur normalisée). Le nombre réel représenté correspond alors à S*(M*2^E).

Exemple : représentation de valeurs décimales en binaire

Une valeur normalisée est une valeur dont la mantisse a le bit de plus fort poids à 1 (sauf pour représenter la valeur 0). Dans l'exemple précédent, la représentation (S, M, E) était à chaque fois normalisée. Il existe différentes variantes pour ce qui est de la manière de représenter des exposants négatifs ou des réels négatifs, mais quelle que soit la manière, les qualités et inconvénients restent à peu près les mêmes.

Exemples de représentation de nombres et d'exposants négatifs:

• sur une certaine variété de machines ayant des mots machine de 36 bits, les nombres réels en simple précision ont 1 bit de signe, 8 bits d'exposant et 27 bits de mantisse. La représentation est en complément à un avec un exposant biaisé. Cela signifie que,

pour un exposant de 0, le champ E contiendra 128,
pour un exposant de 127, le champ E contiendra 255 et
pour un exposant de -128, le champ E contiendra 0.
Si le nombre a un signe négatif, l'ensemble des bits sont inversés.

• sur un co-processeur arithmétique couramment utilisé dans des micro-ordinateurs, les nombres réels sont représentés sur 32 bits avec un bit de signe, un exposant de sept bits en complément à deux et une mantisse en valeur absolue.

Les principales qualités de la représentation en virgule flottante sont :

• l'utilisation optimale de la représentation binaire d'un ordinateur (si les nombres sont normalisés et
• une répartition très étalée de la "gamme" de nombres représentables (typiquement 10⁴⁰ pour de la simple précision et 10¹⁰⁰⁰ pour de la double précision).

Les principaux inconvénients étant que :

• il n'y a pas moyen d'éviter des erreurs d'arrondi à chaque calcul et
• les opérations arithmétiques sont plus complexes que sur des nombres entiers.

Par exemple, il n'est pas du tout certain que l'expression logique

sqr( sqrt(2.0) ) = 2.0

correspondant àsoit vraie

2.3.2. Représentation en virgule fixe

La représentation en virgule fixe consiste à utiliser une représentation similaire aux nombres entiers en attribuant un nombre de "bits" fixes à la partie fractionnaire et un autre nombre de "bits" à la partie entière.

L'avantage principal de cette représentation étant de pouvoir utiliser les opérations arithmétiques des nombres entiers auxquelles s'ajoute l'opération de décalage. Ces opérations sont très efficaces et accélèrent d'autant le calcul.

Les principaux inconvénients sont que la répartition de la "gamme" de nombres représentables est beaucoup plus étroite que pour la virgule flottante (typiquement 10¹⁰ à 10²⁰) et que les erreurs d'arrondis sont aussi inévitables et même s'accumulent beaucoup plus vite.

Exemple : pour des nombres tenant sur 32 bits, on pourrait avoir 1 bit de signe, 23 bits pour la partie entière et 8 bits pour la partie fractionnaire. Le plus grand nombre représentable serait environ 2²³ soit inférieur à 10⁸ et le plus petit nombre représentable serait 2^-8 soit environ 10^-2.

2.3.2.1. Représentation BCD

Il existe une variante de la représentation en virgule fixe qui s'appelle la représentation BCD (Binary Coded Decimal). Elle est surtout utilisée dans les langages à usage commercial (tel que COBOL) et permet de représenter des nombres comme une suite de chiffres allant de 0 à 9, l'emplacement de la virgule étant fourni séparément. L'idée de cette représentation étant de ne pas avoir d'erreur d'arrondi tant que l'on se limite à utiliser des nombres en base 10 ayant un nombre limité de chiffres.

Exemple

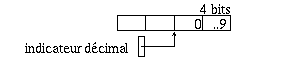
Fig.2.1. Représentation BCD.

Ce qu'il faut retenir de tout cela, c'est que les nombres réels, tels qu'ils sont représentés en machine, n'ont pas les mêmes propriétés qu'en mathématique. Par exemple, (X/Y)*Y n'est pas forcément égal à X.

Les langages FORTRAN, PASCAL et MODULA II, ainsi que beaucoup d'autres langages, n'offrent que la représentation en virgule flottante. ADA et COBOL offrent les deux possibilités. Pour la représentation en virgule fixe, COBOL permet de spécifier le nombre de chiffres significatifs alors que ADA permet de définir l'intervalle de valeurs possibles ainsi que l'écart entre deux valeurs consécutives.

2.4. Compatibilité et conversion de types

Table des matières.

Site Hosting: Bronco